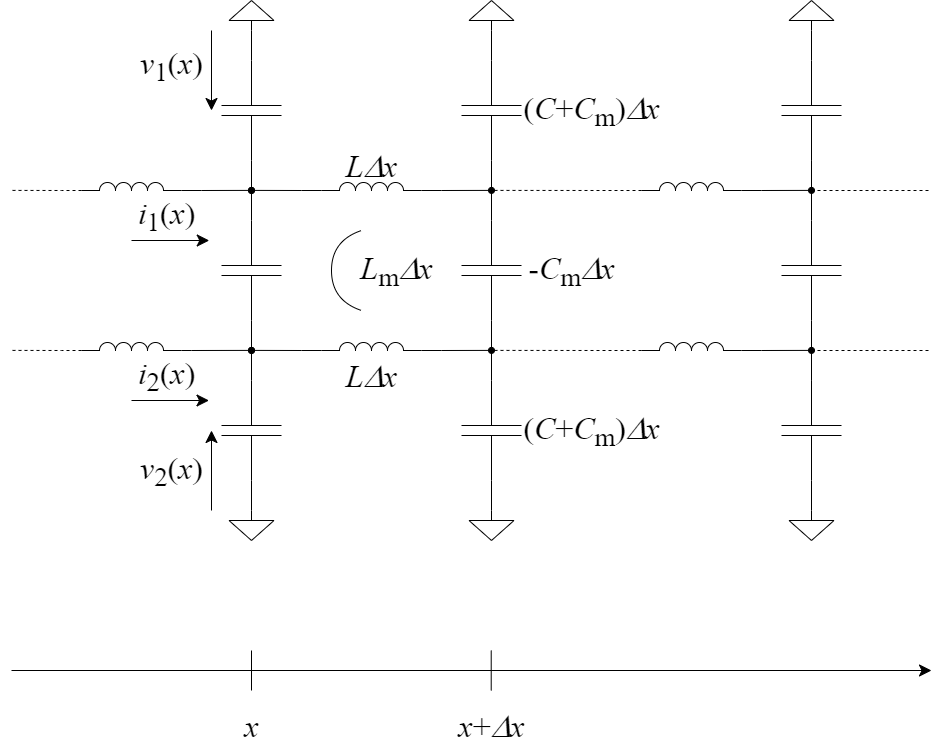
下の図のように2つの伝送線路が相互インダクタンス$L_\mathrm{m}$と相互キャパシタンス$-C_\mathrm{m}$によって結合されているモデルを考えます.(実際の線路では抵抗や漏れコンダクタンスによる損失が生じますがここでは簡単のため無損失線路について考えます.) 線路間のキャパシタンスの符号をどう取るかはいくつかの流派がありますが, 今回は式の対称性をよくして後で気持ち良くなれる[1]ように相互キャパシタンスを$-C_\mathrm{m}$,線路の単位長さあたりのキャパシタンスを$C+C_\mathrm{m}$と置いています. このとき,実際の線路間の相互キャパシタンス$-C_\mathrm{m}$は正の値を取るため$C_\mathrm{m}\leq0$となる点に注意が必要です.
他の回路とのいろいろなことを考えると,線路間のキャパシタンスを正の$C_\mathrm{m}$と取る方が自然です. どちらかというとそっちの方が主流[2]な気もしますが,記事中で統一できていればまあどちらでも良いかな……

この回路の微小区間$\Delta x$における上側の信号線の電圧,電流に注目すると以下の回路方程式が成り立ちます. \begin{align*} v_1(x) - v_1(x+\Delta x) &= L\Delta x\frac{\mathrm{d}i_1}{\mathrm{d}t} + L_\mathrm{m}\Delta x\frac{\mathrm{d}i_2}{\mathrm{d}t}\\ i_1(x) - i_1(x+\Delta x) &= (C+C\mathrm{m})\Delta x\frac{\mathrm{d}v_1}{\mathrm{d}t} - C_\mathrm{m}\Delta x\frac{\mathrm{d}(v_1-v_2)}{\mathrm{d}t}\\ &= C\Delta x\frac{\mathrm{d}v_1}{\mathrm{d}t} + C_\mathrm{m}\Delta x\frac{\mathrm{d}v_2}{\mathrm{d}t} \end{align*} これらの式において$\Delta x\to 0$の極限を取ると \begin{align*} - \frac{\mathrm{\partial}v_1}{\mathrm{\partial}x} &= L\frac{\mathrm{\partial}i_1}{\mathrm{\partial}t} + L_\mathrm{m}\frac{\mathrm{\partial}i_2}{\mathrm{\partial}t}\\ -\frac{\mathrm{\partial}i_1}{\mathrm{\partial}x} &= C\frac{\mathrm{\partial}v_1}{\mathrm{\partial}t} + C_\mathrm{m}\frac{\mathrm{\partial}v_2}{\mathrm{\partial}t} \end{align*} という偏微分方程式が得られます. また,下側の信号線の$v_2,\ i_2$に関しても同様の式を得ることができ,これらを組み合わせると \begin{align*} -\frac{\mathrm{\partial}}{\mathrm{\partial}x}\left( \begin{array}{c} v_1\\ v_2 \end{array}\right)&=\frac{\mathrm{\partial}}{\mathrm{\partial}t}\left( \begin{array}{cc} L& L_\mathrm{m}\\ L_\mathrm{m}& L \end{array}\right)\left( \begin{array}{c} i_1\\ i_2 \end{array}\right)\\ -\frac{\mathrm{\partial}}{\mathrm{\partial}x}\left( \begin{array}{c} i_1\\ i_2 \end{array}\right)&=\frac{\mathrm{\partial}}{\mathrm{\partial}t}\left( \begin{array}{cc} C& C_\mathrm{m}\\ C_\mathrm{m}& C \end{array}\right)\left( \begin{array}{c} v_1\\ v_2 \end{array}\right) \end{align*} が得られます. これが(2導体の)結合線路の電信方程式です. この式は単線路の電信の自然な拡張(個人の感想)であり,信号線が増えた場合$L,\ C$の行列と$v,\ i$のベクトルの次数がそのまま増える形になります.
先述した電信方程式からわかるように,結合線路の一方の導体にかかる電圧,流れる電流は自身の線路だけでなく,もう一方の線路の電圧,電流にも影響されます. このとき,線路の特性は2つの線路を流れる信号が同相,すなわち$v_1=v_2$,$i_1=i_2$となっているとき(偶モード,コモンモード)と信号が逆相,すなわち$v_1=-v_2$,$i_1=-i_2$となっているとき(奇モード,ディファレンシャルモード)の2つの場合(モード)に分解し表現することができます. ここでは線路が偶モードの場合と奇モードの場合の2通りについて特性インピーダンスと位相定数を求めます.
まず偶モードの場合,$v_1=v_2$,$i_1=i_2$が成り立つため,上側の線路に着目した電信方程式は \begin{align*} - \frac{\mathrm{\partial}v_1}{\mathrm{\partial}x} &= L\frac{\mathrm{\partial}i_1}{\mathrm{\partial}t} + L_\mathrm{m}\frac{\mathrm{\partial}i_1}{\mathrm{\partial}t}\\ &= (L+L_\mathrm{m})\frac{\mathrm{\partial}i_1}{\mathrm{\partial}t}\\ -\frac{\mathrm{\partial}i_1}{\mathrm{\partial}x} &= C\frac{\mathrm{\partial}v_1}{\mathrm{\partial}t} + C_\mathrm{m}\frac{\mathrm{\partial}v_1}{\mathrm{\partial}t}\\ &= (C+C_\mathrm{m})\frac{\mathrm{\partial}v_1}{\mathrm{\partial}t} \end{align*} と書けます. この式は$v_1,\ i_1$の2変数しか無く,通常の(単線路の)電信方程式と同じ形をしており,容易に解くことができます. 途中経過は省きますが,このときの線路の特性インピーダンス(偶モードインピーダンス)と位相定数はそれぞれ \begin{align*} Z_\mathrm{e} &= \sqrt{\frac{L+L_\mathrm{m}}{C+C_\mathrm{m}}} = \sqrt{\frac{L+L_\mathrm{m}}{C-|C_\mathrm{m}|}}\\ \beta_\mathrm{e} &= \omega\sqrt{(L+L_\mathrm{m})(C+C_\mathrm{m})} = \omega\sqrt{(L+L_\mathrm{m})(C-|C_\mathrm{m}|)} \end{align*} となります. 一方で奇モードの場合は,$v_1=-v_2$,$i_1=-i_2$となるため,先程と$L_\mathrm{m},\ C_\mathrm{m}$の符号が反転し, \begin{align*} Z_\mathrm{o} &= \sqrt{\frac{L-L_\mathrm{m}}{C-C_\mathrm{m}}} = \sqrt{\frac{L-L_\mathrm{m}}{C+|C_\mathrm{m}|}}\\ \beta_\mathrm{o} &= \omega\sqrt{(L-L_\mathrm{m})(C-C_\mathrm{m})} = \omega\sqrt{(L-L_\mathrm{m})(C+|C_\mathrm{m}|)} \end{align*} となります. 線路が結合しているとき,$L_\mathrm{m}>0,\ -C_\mathrm{m}>0$であるので偶モードインピーダンス$Z_\mathrm{e}$と奇モードインピーダンス$Z_\mathrm{o}$の間には$Z_\mathrm{e} > Z_\mathrm{o}$の関係が成り立ちます.
線路が結合していない($L_\mathrm{m}=0,\ -C_\mathrm{m}=0$)場合の線路の特性インピーダンス$Z_0(:=\sqrt{\frac{L}{C}})$を考えると, 各モードの特性インピーダンスはそれぞれ \begin{eqnarray*} Z_\mathrm{e} &= Z_0\sqrt{\frac{1+L_\mathrm{m}/L}{1-|C_\mathrm{m}|/C}}\\ Z_\mathrm{o} &= Z_0\sqrt{\frac{1-L_\mathrm{m}/L}{1+|C_\mathrm{m}|/C}} \end{eqnarray*} と書けます. ここで$L_\mathrm{m}/L=: k_\mathrm{m}$は2つの線路の磁界による結合係数であり, $|C_\mathrm{m}|/C=: k_\mathrm{c}$は電界による結合係数です. 均一な媒質中ではインダクタンスとキャパシタンスの間に \[\left( \begin{array}{cc} L& L_\mathrm{m}\\ L_\mathrm{m}& L \end{array}\right) = \varepsilon\mu \left( \begin{array}{cc} C& C_\mathrm{m}\\ C_\mathrm{m}& C \end{array}\right)^{-1}\] が成り立つ[3]ため$k_\mathrm{m}=k_\mathrm{ c} =: k$となります. この$k$が結合線路の結合係数であり,シグナルインテグリティ界隈では基礎クロストーク係数と呼ばれるものになります. また,方向性結合器界隈では結合係数をdBで表記した結合度$C := -20\log_{10} k$をよく使います. また,$k=k_\mathrm{m}=k_\mathrm{c}$が成り立つとき,結合線路の位相定数は \[\beta_\mathrm{e}=\beta_\mathrm{o}=\omega\sqrt{(LC)(1+k^2)}\] となり偶モードと奇モードの信号の伝搬速度は等しくなります.
一方で,マイクロストリップ線路のように不均一な媒質中の線路の場合$k_\mathrm{m}\neq k_\mathrm{c}$となります. このとき,各モードの位相定数は \begin{align*} \beta_\mathrm{e} &= \beta_0\sqrt{1+(k_\mathrm{m}-k_\mathrm{c})+k_\mathrm{m}k_\mathrm{c}}\\ \beta_\mathrm{o} &= \beta_0\sqrt{1-(k_\mathrm{m}-k_\mathrm{c})+k_\mathrm{m}k_\mathrm{c}}\\ (\because \beta_\mathrm{0} &= \omega\sqrt{LC}) \end{align*} となり,偶奇モードの信号の伝搬に時間差が生じます. このことは方向性結合器であれば方向性(アイソレーション特性)の悪化,シグナルインテグリティの観点では遠端クロストークの要因となります. この問題を解消するための工夫として,線路にギザギザを設けることで位相速度を補償する[4]等の設計法もありますが,できることなら信号を内層に配置し, 均一なストリップ線路構造とするのが良い気がします(実際にはストリップ線路構造にしても完全には解消できないのですが……)
(均一な媒質中の)結合線路の結合度と特性インピーダンスから偶奇モードのインピーダンスを求めます(逆もしかり).
| 結合度 $C$ [dB] | 偶モードインピーダンス $Z_\mathrm{e}$ [$\Omega$] | |||
| 特性インピーダンス $Z_0$ [$\Omega$] | 奇モードインピーダンス $Z_\mathrm{o}$ [$\Omega$] |
[1] 碓井有三,"2本線路の線路定数、なぜ線路間の容量の Cm が負?," マクニカ,2018.
[2] Inder J. Bahl, Prakash Bhartia, J. R. Hong, and R.K. Mongia "RF and Microwave Coupled-Line Circuits, Second Edition," ARTECH HOUSE, 2007.
[3] Cao Wei, R. F. Harrington, J. R. Mautz, and T.K. Sarkar, “Multiconductor Transmission Lines In Multilayered Dielectric Media,” IEEE Transactions on Microwave Theory and Techniques, vol. 32, no. 4, pp. 439-450, Apr. 1984.
[4] S. Uysal and H. Aghvami, "Synthesis, design, and construction of ultra-wide-band nonuniform quadrature directional couplers in inhomogeneous media," IEEE Transactions on Microwave Theory and Techniques, vol. 37, no. 6, pp. 969-976, June 1989.