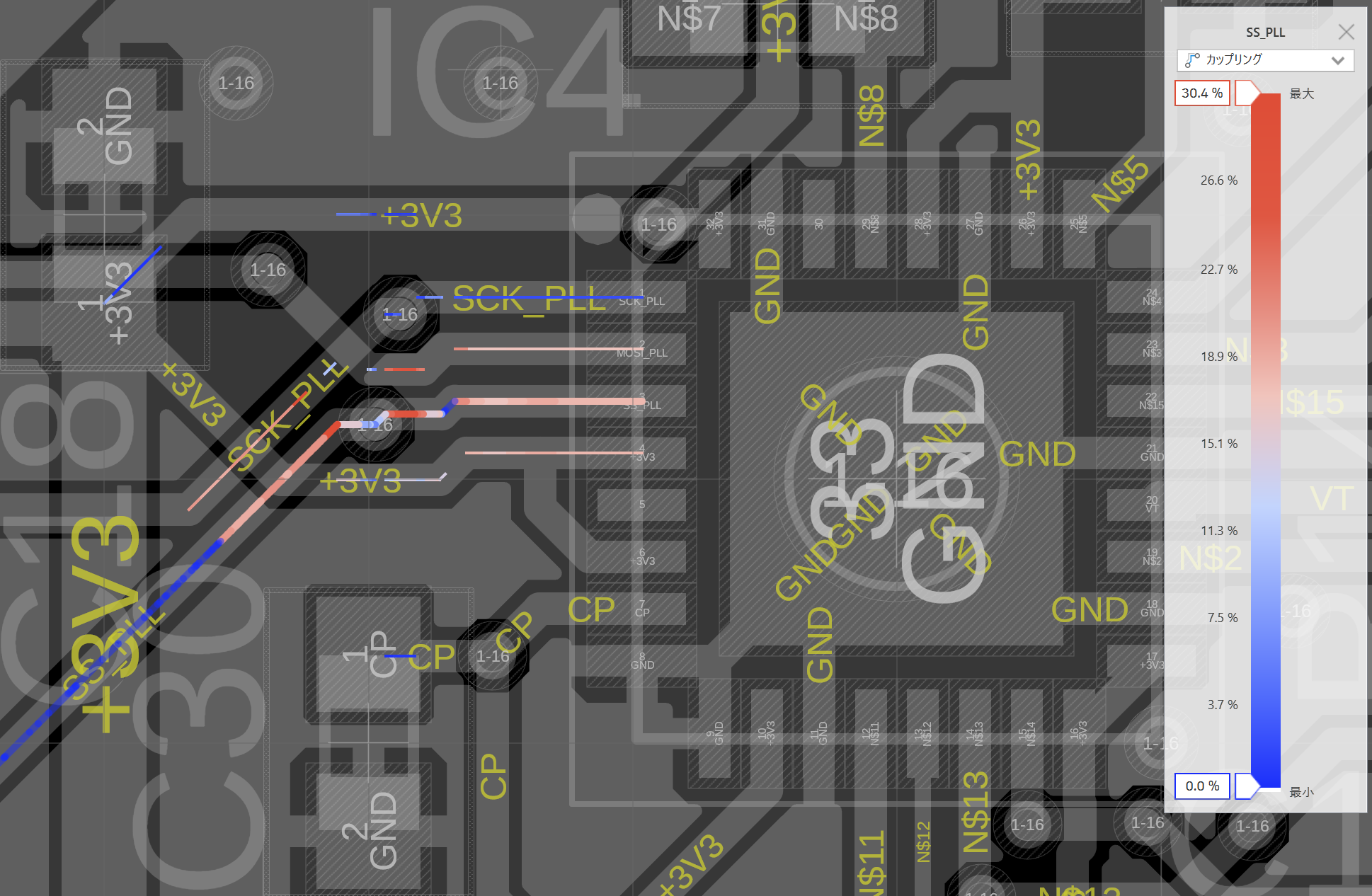
信号を伝える伝送線路の近くに他の線路があると,線路間相互の結合により信号が互いに干渉を与えるクロストークが生じます. 最近Autodesk FusionのSignal Integrity Extensionに線路間の結合を評価できる機能が増え,回路設計時にクロストークの影響を容易に予測できるようになりました(2024年4月~?). この機能では以下の図のように,解析対象とする被害線路(victim)に対して他の線路が加害者(aggressor)としてどの程度影響を与えるのか,色分けして可視化してくれます. このときカラーバーで"カップリング %"という指標が出ていますが,これは何を示す値で,回路の動作として信号波形にどのような影響を与えるのでしょうか.

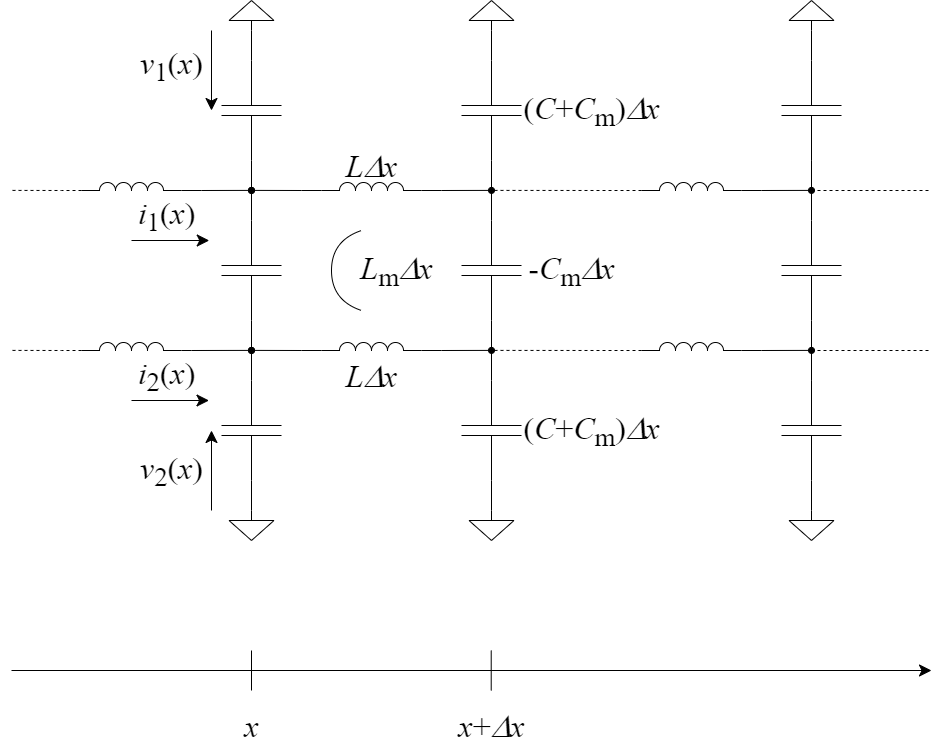
結合線路に関する記事で示した通り,互いに電磁界結合した2本の伝送線路は以下のような回路モデルで表現できます. このとき線路の偶モードインピーダンス$Z_\mathrm{e}$及び奇モードインピーダンス$Z_\mathrm{o}$はそれぞれ \begin{align} Z_\mathrm{e} &= \sqrt{\frac{L+L_\mathrm{m}}{C+C_\mathrm{m}}} = \sqrt{\frac{L+L_\mathrm{m}}{C-|C_\mathrm{m}|}}\nonumber\\ &= Z_0\sqrt{\frac{1+k_\mathrm{m}}{1-k_\mathrm{c}}}\\ Z_\mathrm{o} &= \sqrt{\frac{L-L_\mathrm{m}}{C-C_\mathrm{m}}} = \sqrt{\frac{L-L_\mathrm{m}}{C+|C_\mathrm{m}|}}\nonumber\\ &= Z_0\sqrt{\frac{1-k_\mathrm{m}}{1+k_\mathrm{c}}} \end{align} となります.ただし$Z_0 = \sqrt{L/C},\ k_\mathrm{m}=L_\mathrm{m}/L,\ k_\mathrm{c}=|C_\mathrm{m}|/C$です. (※導出過程は結合線路の記事を見てください.$C_\mathrm{m}$の符号についてもそちらで説明しています.) 更に$k_\mathrm{m}\ll 1,\ k_\mathrm{c}\ll 1$として$(1+x)^n \simeq 1+nx$を使うと \begin{align} Z_\mathrm{e} &\simeq Z_0\left(1+\frac{k_\mathrm{m}}{2}\right)\left(1+\frac{k_\mathrm{c}}{2}\right) &= Z_0\left(1+\frac{k_\mathrm{m}}{2}+\frac{k_\mathrm{c}}{2}\right)\label{ze}\\ Z_\mathrm{o} &\simeq Z_0\left(1-\frac{k_\mathrm{m}}{2}\right)\left(1-\frac{k_\mathrm{c}}{2}\right) &= Z_0\left(1-\frac{k_\mathrm{m}}{2}-\frac{k_\mathrm{c}}{2}\right)\label{zo} \end{align} と書くことができます(後で使います).
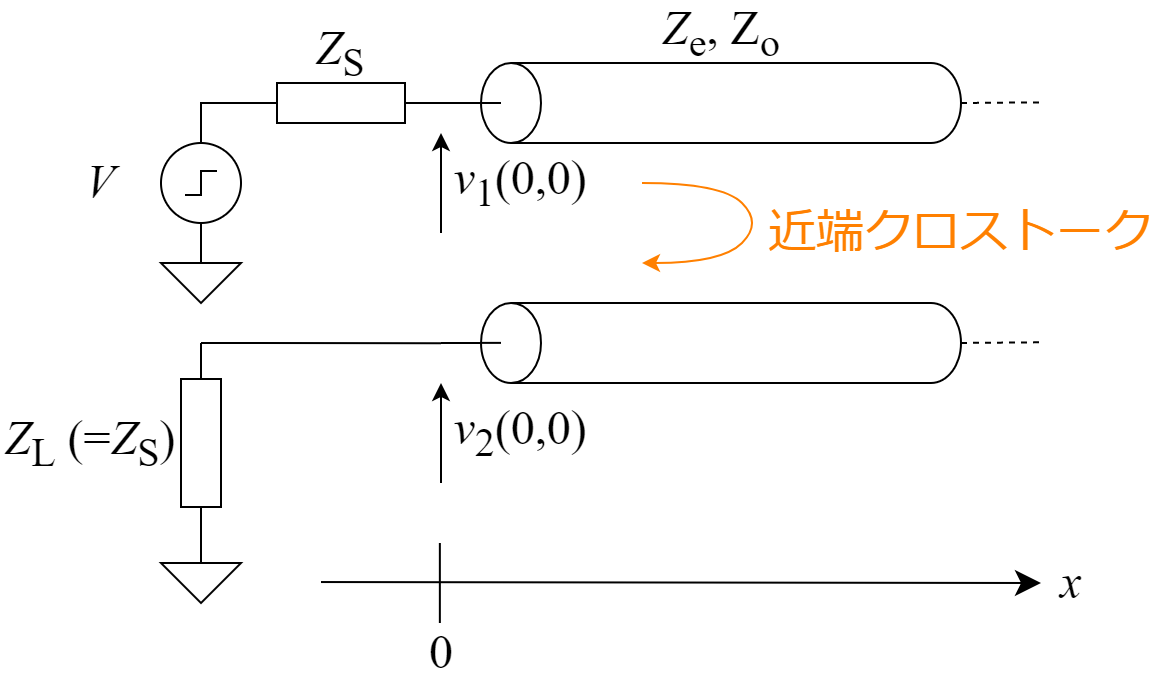
下図に示すように特性インピーダンスが$Z_\mathrm{e},\ Z_\mathrm{o}$の結合線路の一方に$t=0$で立ち上がるステップ信号を入力することを考えます. このとき,他方の線路にはクロストークによりある電圧が誘起されます. 特に図中の電圧電圧$v_2(0,0)$のように送信端($x=0$)側で生じるクロストークを,近端クロストーク(Near-End Closs-Talk: NEXT)と呼び,$v_1(0,0)$に対する$v_2(0,0)$の比を近端クロストーク係数と呼びます. ではこの線路における近端クロストーク係数は具体的にどのような値になるでしょうか.
この↑回路は以下の図のように上下の線路をどちらも$1/2$の振幅で励振した偶モードと,それぞれ$\pm 1/2$の電圧で励振した奇モードの回路の重ね合わせと考えることができます. 偶モードと奇モードの回路の電圧を足すことで上側の線路を励振する電圧は$1/2 V+1/2 V = V$となり,下側の線路は$1/2 V - 1/2 V=0$と終端されることが確認できると思います.
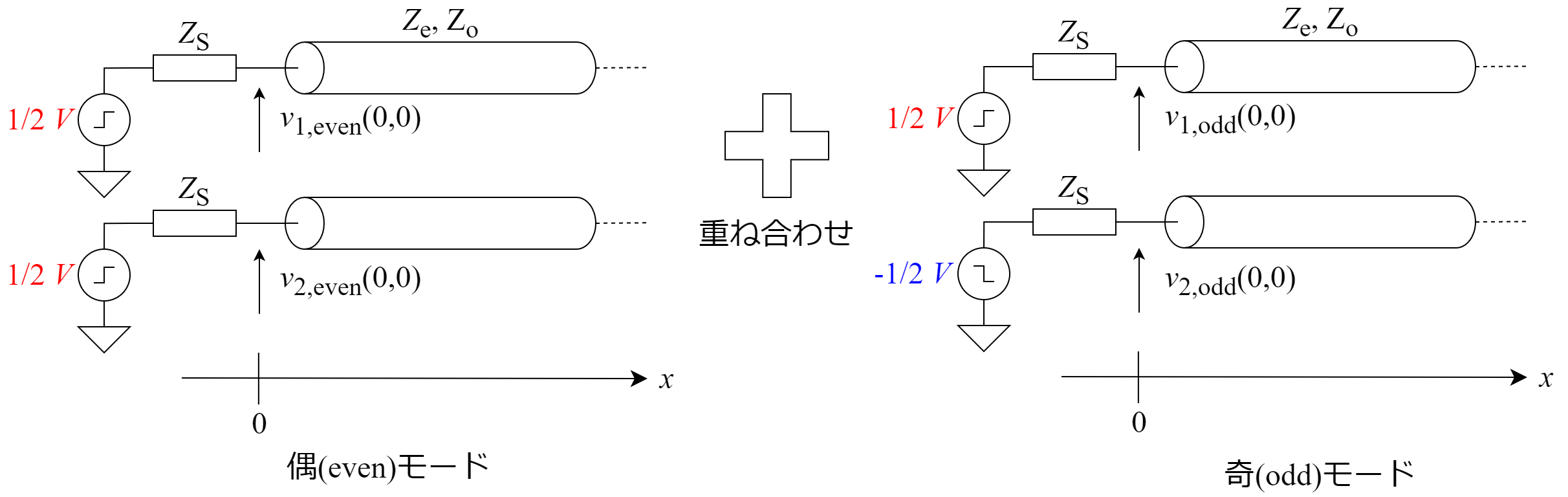
ここで偶モードの場合,信号源インピーダンス$Z_\mathrm{S}$と線路の偶モードインピーダンス$Z_\mathrm{e}$から各線路の$t=0,\ x=0$での電圧はそれぞれ \begin{align} v_\mathrm{1,even}(0,0) &= \frac{1}{2}V\times\frac{Z_\mathrm{e}}{Z_\mathrm{S}+Z_\mathrm{e}}\label{v1e}\\ v_\mathrm{2,even}(0,0) &= \frac{1}{2}V\times\frac{Z_\mathrm{e}}{Z_\mathrm{S}+Z_\mathrm{e}}\label{v2e} \end{align} となり,奇モードの場合は線路の奇モードインピーダンスが$Z_\mathrm{o}$であるから \begin{align} v_\mathrm{1,odd}(0,0) &= \frac{1}{2}V\times\frac{Z_\mathrm{o}}{Z_\mathrm{S}+Z_\mathrm{o}}\label{v1o}\\ v_\mathrm{2,odd}(0,0) &= -\frac{1}{2}V\times\frac{Z_\mathrm{o}}{Z_\mathrm{S}+Z_\mathrm{o}}\label{v2o} \end{align} となります.
式(\ref{v1e},\ref{v1o})より$v_1(0,0)$は \begin{align} v_1(0,0) = v_\mathrm{1,even} + v_\mathrm{1,odd} &= \frac{1}{2}V\left(\frac{Z_\mathrm{e}}{Z_\mathrm{S}+Z_\mathrm{e}}+\frac{Z_\mathrm{o}}{Z_\mathrm{S}+Z_\mathrm{o}}\right)\nonumber\\ &= \frac{1}{2}V\frac{Z_\mathrm{S}(Z_\mathrm{e}+Z_\mathrm{o})+2Z_\mathrm{e}Z_\mathrm{o}}{(Z_\mathrm{S}+Z_\mathrm{o})(Z_\mathrm{S}+Z_\mathrm{e})}\label{v1} \end{align} 式(\ref{v2e},\ref{v2o})より$v_2(0,0)$は \begin{align} v_2(0,0) = v_\mathrm{2,even} + v_\mathrm{2,odd} &= \frac{1}{2}V\left(\frac{Z_\mathrm{e}}{Z_\mathrm{S}+Z_\mathrm{e}}-\frac{Z_\mathrm{o}}{Z_\mathrm{S}+Z_\mathrm{o}}\right)\nonumber\\ &= \frac{1}{2}V\frac{Z_\mathrm{S}(Z_\mathrm{e}-Z_\mathrm{o})}{(Z_\mathrm{S}+Z_\mathrm{o})(Z_\mathrm{S}+Z_\mathrm{e})}\label{v2} \end{align} です.
ここで$Z_\mathrm{L}=Z_\mathrm{S}=\sqrt{Z_\mathrm{e}Z_\mathrm{o}}$と整合されているとすると式(\ref{v1})は \begin{align} v_1(0,0) &= \frac{1}{2}V\frac{\sqrt{Z_\mathrm{e}Z_\mathrm{o}}(Z_\mathrm{e}+Z_\mathrm{o})+2Z_\mathrm{e}Z_\mathrm{o}}{(\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+Z_\mathrm{o})(\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+Z_\mathrm{e})} = \frac{1}{2}V\frac{Z_\mathrm{e}\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+Z_\mathrm{o}\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+2Z_\mathrm{e}Z_\mathrm{o}}{Z_\mathrm{e}\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+Z_\mathrm{o}\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+2Z_\mathrm{e}Z_\mathrm{o}}\nonumber\\ &= \frac{1}{2}V\label{v1_2} \end{align} となり,電源電圧の$1/2$の電圧となることがわかります. また$v_2(0,0)$は \begin{align} v_2(0,0) &= \frac{1}{2}V\frac{\sqrt{Z_\mathrm{e}Z_\mathrm{o}}(Z_\mathrm{e}-Z_\mathrm{o})}{(\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+Z_\mathrm{o})(\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+Z_\mathrm{e})}\nonumber\\ &= \frac{1}{2}V\frac{Z_\mathrm{e}-Z_\mathrm{o}}{2\sqrt{Z_\mathrm{e}Z_\mathrm{o}}+Z_\mathrm{e}+Z_\mathrm{o}}\label{v2_2} \end{align} となりますが,ここで線路間の結合が弱い場合,すなわち$Z_\mathrm{e}\simeq Z_\mathrm{o}$であれば$\sqrt{Z_\mathrm{e}Z_\mathrm{o}}\simeq \frac{Z_\mathrm{e}+Z_\mathrm{o}}{2}$が成り立つので式(\ref{v2_2})に代入すると最終的に$v_2(0,0)$は \begin{align} v_2(0,0) &= \frac{1}{4}V\frac{Z_\mathrm{e}-Z_\mathrm{o}}{Z_\mathrm{e}+Z_\mathrm{o}}\nonumber\\ &= \frac{1}{2}\frac{Z_\mathrm{e}-Z_\mathrm{o}}{Z_\mathrm{e}+Z_\mathrm{o}}v_1(0,0) \end{align} と整理できます. 従って特性インピーダンスが$Z_\mathrm{e},\ Z_\mathrm{o}$の結合線路における近端クロストーク係数は \begin{equation} k_\mathrm{b} = \frac{v_2(0,0)}{v_1(0,0)} = \frac{1}{2}\frac{Z_\mathrm{e}-Z_\mathrm{o}}{Z_\mathrm{e}+Z_\mathrm{o}} \end{equation} となります.
近端クロストーク係数のうち$\frac{Z_\mathrm{e}-Z_\mathrm{o}}{Z_\mathrm{e}+Z_\mathrm{o}}$の部分を基礎クロストーク係数$\xi$と呼びます. つまり$k_\mathrm{b} = \xi/2$です. 冒頭で示したAutodesk Fusionが解析してくれる"カップリング %"はどうやらこの基礎クロストーク係数を指しているようです. 式(\ref{ze},\ref{zo})に示した$Z_\mathrm{e},\ Z_\mathrm{o}$を使うと基礎クロストーク係数は \begin{align} \xi &= \frac{Z_\mathrm{e}-Z_\mathrm{o}}{Z_\mathrm{e}+Z_\mathrm{o}}\nonumber\\ &= \frac{Z_0(k_\mathrm{m}+k_\mathrm{c})}{2Z_0} = \frac{1}{2}(k_\mathrm{m}+k_\mathrm{c}) \end{align}
と書け,電界による結合係数$k_\mathrm{c}$と磁界による結合係数$k_\mathrm{m}$の平均となることがわかります.ここまでの議論では線路間の結合が弱く$Z_\mathrm{e}\simeq Z_\mathrm{o}$であるとして相乗平均を相加平均に置き換え,また$Z_\mathrm{e},\ Z_\mathrm{o}$の式についても$k_\mathrm{m}\ll 1,\ k_\mathrm{c}\ll 1$であるとした近似を用いています. つまり,結合が強い線路(密結合線路)の場合,基礎クロストーク係数はこの式の通りではありません.クロストークを低減するためにも三つの密(密接,密集,密結合)を避けた配線を心掛けるのが良いと思います. ちなみに,基礎クロストーク係数について$k_\mathrm{m}\neq k_\mathrm{c}$であるとして式を示していますが,$k_\mathrm{m}\neq k_\mathrm{c}$の場合$Z_\mathrm{L}=\sqrt{Z_\mathrm{e}Z_\mathrm{o}}$で完全に整合を取ることができず, また,遠端クロストーク(Far-End Closs-Talk: FEXT)が生じます. 均一な媒質中の線路では$k_\mathrm{m}=k_\mathrm{c}$となるため密閉(内層のストリップ線路にする)ことはクロストーク対策としてはむしろアリなのではと思います.